| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 데이터불균형
- DBSCAN
- 독립표본
- opencv
- pandas
- ADsP
- 대응표본
- 워드클라우드
- t-test
- dataframe
- 데이터분석준전문가
- 주성분분석
- 오버샘플링
- 파이썬
- iloc
- numpy
- Python
- 데이터분석
- LDA
- 빅데이터분석기사
- 텍스트분석
- 언더샘플링
- 크롤링
- ADP
- Lambda
- PCA
- 군집화
- 데이터분석전문가
- 빅데이터
- datascience
Data Science LAB
[Python] 데이터 에듀 ADP 실기 모의고사 1회 2번 파이썬 ver (통계분석) 본문
사용 데이터 : FIFA.csv
FIFA 데이터는 가상의 온라인 축구게임에 등장하는 축구 선수의 주요 특징과 신체 정보에 대한 데이터이며, 변수 설명은 아래와 같다.
| 변수 | 데이터형태 |
| ID | 수치형 |
| Age | 수치형 |
| Nationality | 범주형 |
| Overall | 수치형 |
| Club | 범주형 |
| Preferred Foot | 범주형 |
| Work Rate | 범주형 |
| Position | 범주형 |
| Jersey Number | 수치형 |
| Contract Valid Until | 수치형 |
| Height | 문자형 |
| Weight_lb | 수치형 |
| Release_Clause | 수치형 |
| Value | 수치형 |
| Wage | 수치형 |
1. FIFA 데이터에서 각 선수의 키는 Height변수에 피트와 인치로 입력되어 있습니다. 이를 cm로 변환하여 새로운 변수 Height_cm을 생성하시오.(" ' " 앞의 숫자는 피트이며, 뒤의 숫자는 인치, 1피트 = 30cm, 1인치 = 2.5cm)
import pandas as pd
import numpy as np
fifa = pd.read_csv(r'../data/FIFA.csv',encoding='euc-kr')
fifa.head()
def createcm(x):
x_list = x.split("'")
cm = int(x_list[0]) * 30 + int(x_list[1]) * 2.5
return cm
fifa['Height_cm'] = fifa['Height'].apply(createcm)
fifa.head()
" ' " 을 기준으로 분류한 뒤 30과 2.5를 각각 곱해 cm단위로 변환
2. 포지션을 의미하는 Position변수를 아래 표를 참고하여 "Forward", "Midfielder", "Defender", "GoalKeeper" 로 재범주화하고, factor형으로 변환하여 Position_Class라는 변수를 생성하고 저장하시오.
| Forward | LS, ST, RS, LW, LF, CF, RF, RW |
| Midfielder | LAM, CAM, RAM, LM, LCM, CM, RCM, RM |
| Defender | LWB, LDM, CDM, RDM, RWB, LB, LCB, CB, RCB, RB |
| GoalKeeper | GK |
p_dict = { 'Forward' : ['LS', 'ST', 'RS', 'LW', 'LF', 'CF', 'RF', 'RW'],
'MidFielder' : ['LAM', 'CAM', 'RAM', 'LM', 'LCM', 'CM', 'RCM', 'RM'],
'Defender': ['LWB', 'LDM', 'CDM', 'RDM', 'RWB', 'LB', 'LCB', 'CB', 'RCB', 'RB'],
'GoalKeeper' :['GK']}
def get_key(x):
for key, value in p_dict.items():
if x in value:
y = key
return y
딕셔너리 형태로 데이터를 정의한 다음, key값을 반환하는 함수 생성
fifa['Position_class'] = fifa['Position'].apply(get_key)
fifa.head()
Position 변수에 적용하여 새로운 Position_Class 열 생성
3. 새로 생성한 Position_Class 변수의 각 범주에 따른 Value 변수 평균값의 차이를 비교하는 일원배치 분산분석을 수행하고 결과를 해석하시오. (데이터는 등분산성을 만족한다고 가정) 그리고 평균값의 차이가 통계적으로 유의하다면 사후검정을 수행하고 설명하시오.
import scipy.stats as stats
import pingouin as pg
from statsmodels.stats.multicomp import pairwise_tukeyhsd
from statsmodels.stats.multicomp import MultiComparison
fifa.Position_class.value_counts()
# Defender 6763
# MidFielder 4935
# Forward 3044
# GoalKeeper 1900
fifa['Position_class'].unique()
# array(['Forward', 'GoalKeeper', 'MidFielder', 'Defender'], dtype=object)
# 포지션별 변수 할당
position_list = fifa['Position_class'].unique()
forward = fifa[fifa['Position_class'] == position_list[0]]['Value']
goalkeeper = fifa[fifa['Position_class'] == position_list[1]]['Value']
midfielder = fifa[fifa['Position_class'] == position_list[2]]['Value']
defender = fifa[fifa['Position_class'] == position_list[3]]['Value']변수의 데이터가 충분히 크기 때문에 정규성을 만족한다고 판단
- 귀무가설 : 4가지 포지션에 대해 Value의 평균은 같다.
- 대립가설 : 적어도 하나의 포지션에 대한 Value의 평균값에는 차이가 있다.
stats.f_oneway(forward, goalkeeper, midfielder, defender)
# F_onewayResult(statistic=41.87390580849466, pvalue=5.988667429906719e-27)p-value가 0.05보다 작기 때문에 유의수준 5%에서 귀무가설을 기각한다. 즉 적어도 하나의 포지션의 Value 평균값에는 차이가 존재한다고 판단한다. -> 사후검정 필요
mc = MultiComparison(data = fifa['Value'], groups=fifa['Position_class'])
tuekeyhsd = mc.tukeyhsd(alpha=0.05)
fig = tuekeyhsd.plot_simultaneous()
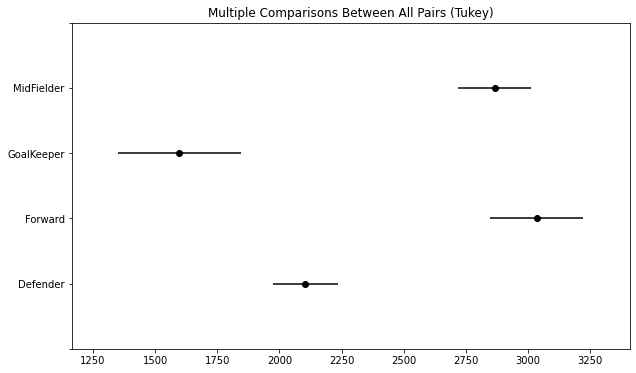
시각화 결과 육안으로도 각각의 평균에 차이가 존재함을 알 수 있음
tuekeyhsd.summary()
Forward와 Midfielder를 제외한 모든 변수간에 차이가 있다고 판단했다. 즉, 거의 모든 변수들에 차이가 존재한다고 판단한다.
4. Preferred Foot과 Position_Class 변수에 따라 Value의 차이가 있는지를 알아보기 위해 이원 배치 분산 분석을 수행하고, 결과를 해석하시오.
귀무가설
- Preferred Foot 변수에 따른 Value 값 에는 차이가 없다.
- Position_Class 변수에 따른 Value 값에는 차이가 없다.
- Preferred Foot과 Position_Class변수의 상호작용 효과가 없다.
대립가설
- Preferred Foot 변수에 따른 Value 값에는 차이가 있다.
- Position_Class 변수에 따른 Value 값에는 차이가 있다.
- Preferred Foot과 Position_Class변수의 상호작용 효과가 있다.anova_data = fifa[['Position_class', 'Preferred_Foot', 'Value']]
anova_data.info()
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
formula = 'Value ~ C(Preferred_Foot) + C(Position_class) + C(Preferred_Foot) : C(Position_class)'
model = ols(formula, anova_data).fit()
aov_table = anova_lm(model, typ=2)
aov_table
- Preferred_Foot 변수의 종속변수에 미치는 영향을 검정한 결과, p-value가 0.05보다 작으므로 귀무가설을 기각한다. 따라서 Preferred_Foot에 따른 Value 차이가 존재한다고 판단
- Position_class 변수의 종속변수에 미치는 영향을 검정한 결과, p-value가 0.05보다 작으므로 귀무가설을 기각한다. 따라서 Position_class에 따른 Value 차이가 존재한다고 판단
- 두 변수의 교호작용에 대해 검정한 결과 p-value가 0.05보다 작으므로 귀무가설을 기각한다. 따라서 두 변수에서 교호작용이 존재한다는 것을 알 수 있다.
5. Age, Overall, Wage, Height_cm, Weight_lb가 Value에 영향을 미치는지 알아보는 회귀분석을 단계적 선택법을 사용하여 수행하고 결과를 해석하시오.
import statsmodels.api as sm
import statsmodels.formula.api as smf
model = smf.ols(formula='Value ~ Age + Overall + Wage + Height_cm + Weight_lb', data=fifa)
result = model.fit()
result.summary()
# 다중공선성 파악
fifa[['Age','Overall', 'Wage', 'Height_cm', 'Weight_lb']].corr()
크게 상관관계가 있는 변수는 존재하지 않음
from patsy import dmatrices
from statsmodels.stats.outliers_influence import variance_inflation_factor
y,X = dmatrices('Value ~ Age + Overall + Wage + Height_cm + Weight_lb', data=fifa, return_type='dataframe')
#독립변수끼리의 VIF값을 계산하여 데이터프레임으로 반환
vif_list = []
for i in range(1,len(X.columns)):
vif_list.append([variance_inflation_factor(X.values, i), X.columns[i]])
pd.DataFrame(vif_list, columns = ['vif', 'variable'])
import time
import itertools
def processSubset(X,y, feature_set):
model = sm.OLS(y, X[list(feature_set)])
regr = model.fit()
AIC = regr.aic
return {'model':regr, 'AIC':AIC}
#전진선택법
def forward(X,y,predictors):
remaining_predictors = [p for p in X.columns.difference(['Intercept']) if p not in predictors]
results = []
for p in remaining_predictors:
results.append(processSubset(X=X, y=y, feature_set=predictors + [p] + ['Intercept']))
models = pd.DataFrame(results)
best_model = models.loc[models['AIC'].argmin()]
print('Proceed', models.shape[0], 'models on', len(predictors)+1, 'predictors in')
print('Selected predictors:', best_model['model'].model.exog_names, 'AIC:', best_model[0])
return best_model
#후진소거법
def backward(X,y,predictors):
tic = time.time()
results = []
for combo in itertools.combinations(predictors, len(predictors) -1):
results.append(processSubset(X=X, y=y, feature_set=list(combo) + ['Intercept']))
models = pd.DataFrame(results)
best_model= models.loc[models['AIC'].argmin()]
toc = time.time()
print('Processed', models.shape[0], 'models on', len(predictors)-1, 'predictors in', (toc-tic))
print('Selected predictors:', best_model['model'].model.exog_names,
'AIC:', best_model[0])
return best_model
#단계적 선택법
def Stepwise_model(X,y):
Stepmodels = pd.DataFrame(columns=['AIC','model'])
tic = time.time()
predictors = []
Smodel_before = processSubset(X,y, predictors+['Intercept'])['AIC']
for i in range(1, len(X.columns.difference(['Intercept']))+1):
Forward_result = forward(X=X, y=y, predictors=predictors)
print('forward')
Stepmodels.loc[i] = Forward_result
predictors = Stepmodels.loc[i]['model'].model.exog_names
predictors = [k for k in predictors if k!= 'Intercept']
Backward_result = backward(X=X, y=y, predictors=predictors)
if Backward_result['AIC'] < Forward_result['AIC']:
Stepmodels.loc[i] = Backward_result
predictors = Stepmodels.loc[i]['model'].model.exog_names
Smodel_before = Stepmodels.loc[i]['AIC']
predictors = [k for k in predictors if k!='Intercept']
print('backward')
if Stepmodels.loc[i]['AIC'] > Smodel_before:
break
else:
Smodel_before = Stepmodels.loc[i]['AIC']
toc = time.time()
print('Total elapsed time : ',(toc-tic), 'seconds')
return (Stepmodels['model'][len(Stepmodels['model'])])Stepwise_best_model = Stepwise_model(X=X,y=y)
Stepwise_best_model.summary()
- Wage, Overall, Age, Height_cm이 포함된 다중 선형 회귀모델을 선택하였다. R2값이 0.791로 모델이 전체 데이터의 약 79%를 설명할 수 있다.
- 회귀식 : y = 184.18 Wage + 241.35 Overall - 202.16 Age - 8.44 Height_cm - 8690.82
- 회귀식에서 가장 큰 영향을 주는 변수는 Overall이라고 할 수 있다.
'adp 실기 > 기출문제' 카테고리의 다른 글
| [Python] 데이터 에듀 ADP 실기 모의고사 2회 3번 파이썬 ver. (비정형 데이터마이닝) (0) | 2022.09.04 |
|---|---|
| [Python] 데이터 에듀 ADP 실기 모의고사 2회 2번 파이썬 ver. (정형데이터마이닝) (0) | 2022.09.03 |
| [Python] 데이터 에듀 ADP 실기 모의고사 2회 1번 파이썬 ver. (통계분석) (0) | 2022.09.01 |
| [Python] 데이터 에듀 ADP 실기 모의고사 1회 3번 파이썬 ver. (비정형 텍스트마이닝) (0) | 2022.08.31 |
| [Python] 데이터에듀 ADP 실기 모의고사 1회 1번 파이썬 ver.(정형 데이터마이닝) (0) | 2022.08.29 |




