| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- 텍스트분석
- LDA
- opencv
- 대응표본
- t-test
- ADsP
- 데이터불균형
- 데이터분석준전문가
- 데이터분석
- 파이썬
- iloc
- numpy
- PCA
- 워드클라우드
- DBSCAN
- pandas
- 독립표본
- 빅데이터
- 데이터분석전문가
- 빅데이터분석기사
- dataframe
- datascience
- 군집화
- 크롤링
- 주성분분석
- 오버샘플링
- Python
- ADP
- 언더샘플링
- Lambda
Archives
Data Science LAB
[Deep Learning] 활성화 함수 종류 및 비교 정리 본문
728x90
1. 활성화 함수(Activation Function) 의미
딥러닝 네트워크에서 노드에 입력된 값들을 비선형 함수에 통과시킨 후 다음 레이어로 전달하는데, 이 때 사용하는 함수를 의미한다. 선형 함수가 아닌 비선형 함수를 사용하는 이유는 딥러닝 모델의 레이어 층을 깊게 가져갈 수 있기 때문이다.
활성화 함수는 입력 신호와 편향의 총합을 계산하여 다음 레이어로 어떻게 출력할 지를 결정한다. 이때 설정한 임계값을 경계로 출력값이 바뀌게 된다.
2. 활성화 함수의 종류
1 ) Sigmoid
- Logistic 함수라고 불리기도 하며 x의 값에 따라 0~1 사이의 값을 출력하는 함수이다.
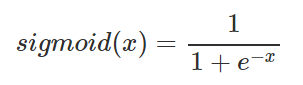
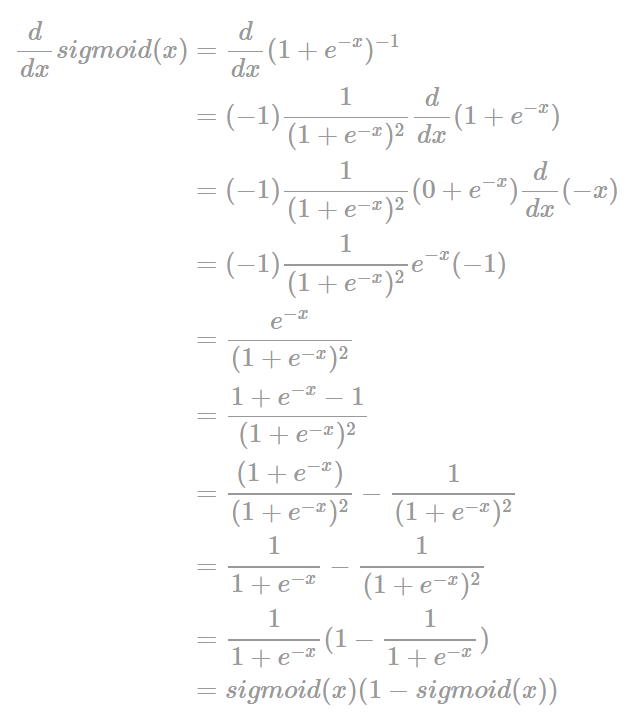
- 파이썬 구현
def sigmoid(x):
return 1 / (1 + np.exp(-x))

- sigmoid 특징
- 음수 값을 0에 가깝게 표현하기 때문에 입력 값이 최종 레이어에서 미치는 영향이 적어지는 Vanishing Gradient Problem 발생
- 미분 계수의 최대값이 0.25이기 때문에 학습을 위해 Back-propagation을 계산하는 과정에서 활성화 함수의 미분 값을 곱하는 과정이 포함되는데, sigmoid함수의 경우 은닉층의 깊이가 깊으면 오차율을 계산하기 어려움
- 중심이 0이 아니기 때문에 학습이 느려질 수 있는 단점
- 한 노드에서 모든 파라미터의 미분 값은 모두 같은 부호이기 때문에 같은 방향으로 업데이트되는 과정은 학습을 지그재그 형태로 만듦
- 미분 결과가 간결하고 사용하기 쉬움
- 모든 실수 값을 0보다 크고 1보다 작은 미분 가능한 수로 변환하는 특징 때문에 Logistic Classification과 같은 분류 문제에 자주 사용
- return 값이 확률 값이기 때문에 결과를 확률로 해석하기 유용
2) Hyperbolic Tangent 함수 (하이퍼볼릭, tanh)
- 쌍곡선 함수 중 하나로, Sigmoid의 단점을 보완한 함수이다.

- 파이썬 구현
def tanh(x):
p_exp_x = np.exp(x)
m_exp_x = np.exp(-x)
y = (p_exp_x - m_exp_x) / (p_exp_x + m_exp_x)
return y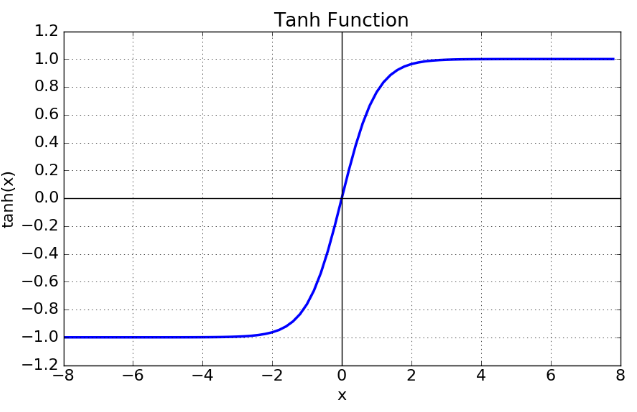
- tanh 특징
- 함수의 중심점을 0으로 설정해 sigmoid의 단점인 최적화 과정에서 속도가 느린 단점을 보완함
- 기울기가 양수와 음수 모두 나올 수 있기 때문에 sigmoid보다 학습 효율성이 뛰어남
- sigmoid에 비해 범위가 넓기 때문에 출력의 변화폭이 더 크고 Vanishing Gradient 문제가 더 적음
- 미분 함수에 대해 일정 값 이상에서 미분 값이 소실되는 Vanishing Gradient은 여전히 남아있음
3) ReLU
- 가장 많이 사용되는 활성화 함수 중 하나로 입력이 0 이상이면 그대로 출력, 0 이하이면 0을 출력하는 함수이다.
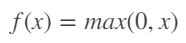
- 파이썬 구현
def relu(x):
return np.maximum(0,x)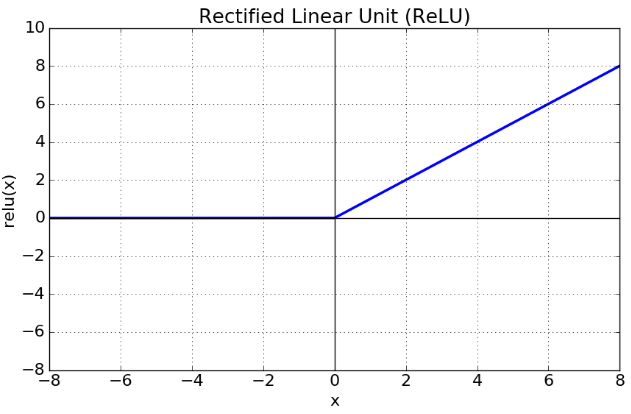
- ReLU 특징
- x가 0보다 크면 기울기가 1인 직선, 0보다 작으면 함수 값이 0이 된다. 이는 0보다 작은 값들에서 뉴런이 죽을 수 있는 단점 (죽은 relu 문제)
- sigmoid, tanh 함수보다 학습이 빠르고 구현이 간단함
4) Leaky Relu
- 0보다 작거나 같을 때 0을 곱하는 것이 아니라 x에 0.01을 곱한 작은 양의 기울기를 사용함
- 죽은 relu 문제를 해결하기 위해 등장
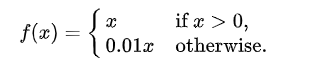
5) PReLU
- x가 양수일 때에는 x값을 그대로 도출, 그외에는 ax값을 도출 (a는 다른 신경망 매개변수와 함께 학습되는 파라미터)
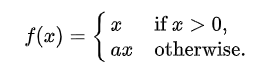
728x90
'🧠 Deep Learning' 카테고리의 다른 글
| [Deep Learning] 딥러닝에서 super().__init__ 사용 (클래스 상속) (0) | 2022.12.07 |
|---|---|
| [Deep Learning] Tensorflow에서 Sequential 모델 생성하는 법 (0) | 2022.11.24 |
| [Deep Learning] 출력층 설계 (softmax, 항등 함수) (0) | 2022.11.23 |
| [Deep Learning] 최적화 방법 비교 (SGD, Momentum, AdaGrad, Adam (0) | 2022.11.18 |
| Deep Learning과 Machine Learning 차이점 (0) | 2022.02.13 |
Comments




