[Python] 데이터 에듀 ADP 실기 모의고사 2회 1번 파이썬 ver. (통계분석)

사용 데이터 : Admission.csv

변수	데이터 형태	설명
GRE	수치형	GRE 점수
TOEFL	수치형	TOEFL 점수
Univ_Rating	수치형	대학교 등급(1~5등급)
SOP	수치형	자기소개서 점수
LOR	수치형	추천서 점수
CGPA	수치형	평점평균
Research	범주형	연구 실적유무(0 : 없음, 1 : 있음)
Chance_of_Admit	수치형	입학 허가 확률

 

 

import pandas as pd
import numpy as np

df = pd.read_csv('../data/Admission.csv')
df.head()

 

 

1. 종속변수인 Chance_of+adimit와 독립변수 (GRE, TOEFL, Univ_Rating, SOP, LOR, CGPA)에 대해 피어슨 상관관계 분석을 수행하고 그래프를 이용하여 분석결과를 설명하시오.

import matplotlib.pyplot as plt
import seaborn as sns

df_corr = df.drop(columns='Research').corr(method='pearson')
sns.heatmap(df_corr, xticklabels=df_corr.columns, 
            yticklabels=df_corr.columns,
            cmap='RdBu', annot=True)
plt.show()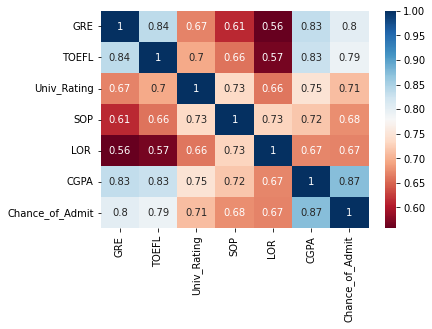

피어슨 상관관계 분석 결과 GRE, TOEFL, CGPA, Univ_Rating 변수가 종속변수 Chance_of_Admitr와 양의 상관관계를 갖는다고 판단함, 그 중 CGPA 변수의 상관계수가 0.87로 가장 많은 상관관계를 가짐

 

 

2. GRE, TOEFL, Univ_Rating, Sop, LOR, CGPA, Research가 Chance_of_Admit에 영향을 미치는지 알아보는 회귀분석을 단계적 선택법을 사용하여 수행하고 결과를 해석하시오.

import time 
import itertools
import statsmodels.api as sm
import statsmodels.formula.api as smf

def processSubset(X,y, feature_set):
    model = sm.OLS(y, X[list(feature_set)])
    regr = model.fit()
    AIC = regr.aic
    return {'model':regr, 'AIC':AIC}

#전진선택법
def forward(X,y,predictors):
    remaining_predictors = [p for p in X.columns.difference(['Intercept']) if p not in predictors]
    results = []
    
    for p in remaining_predictors:
        results.append(processSubset(X=X, y=y, feature_set=predictors + [p] + ['Intercept']))
        
    models = pd.DataFrame(results)
    
    best_model = models.loc[models['AIC'].argmin()]
    print('Proceed', models.shape[0], 'models on', len(predictors)+1, 'predictors in')
    print('Selected predictors:', best_model['model'].model.exog_names, 'AIC:', best_model[0])
    return best_model

#후진소거법
def backward(X,y,predictors):
    tic = time.time()
    results = []
    
    for combo in itertools.combinations(predictors, len(predictors) -1):
        results.append(processSubset(X=X, y=y, feature_set=list(combo) + ['Intercept']))
    
    models = pd.DataFrame(results)
    best_model= models.loc[models['AIC'].argmin()]
    toc = time.time()
    
    print('Processed', models.shape[0], 'models on', len(predictors)-1, 'predictors in', (toc-tic))
    print('Selected predictors:', best_model['model'].model.exog_names,
          'AIC:', best_model[0])
    return best_model

#단계적 선택법
def Stepwise_model(X,y):
    Stepmodels = pd.DataFrame(columns=['AIC','model'])
    tic = time.time()
    predictors = []
    Smodel_before = processSubset(X,y, predictors+['Intercept'])['AIC']
    
    for i in range(1, len(X.columns.difference(['Intercept']))+1):
        Forward_result = forward(X=X, y=y, predictors=predictors)
        print('forward')
        Stepmodels.loc[i] = Forward_result
        predictors = Stepmodels.loc[i]['model'].model.exog_names
        predictors = [k for k in predictors if k!= 'Intercept']
        Backward_result = backward(X=X, y=y, predictors=predictors)
        
        if Backward_result['AIC'] < Forward_result['AIC']:
            Stepmodels.loc[i] = Backward_result
            predictors = Stepmodels.loc[i]['model'].model.exog_names
            Smodel_before = Stepmodels.loc[i]['AIC']
            predictors = [k for k in predictors if k!='Intercept']
            print('backward')
            
        if Stepmodels.loc[i]['AIC'] > Smodel_before:
            break
        
        else:
            Smodel_before = Stepmodels.loc[i]['AIC']
            
    toc = time.time()
    print('Total elapsed time : ',(toc-tic), 'seconds') 
    
    return (Stepmodels['model'][len(Stepmodels['model'])])

 

회귀모델 생성

 

k = df.columns.values.tolist()
k = ' '.join(k).split()
df.columns = ' '.join(df.columns.values).split()

 

LOR 변수의 컬럼명에 공백이 있어서 회귀모델 생성에 에러 발생 -> 모든 컬럼명의 공백을 제거해줌

 

from patsy import dmatrices

y,X = dmatrices('Chance_of_Admit ~ GRE + TOEFL + Univ_Rating + SOP + LOR + CGPA + Research', data = df, return_type='dataframe')
Stepwise_best_model = Stepwise_model(X=X,y=y)
Stepwise_best_model.summary()

 

- 생성된 모델의 수정된 R-square 값은 0.8으로 전체의 80%를 설명할 수 있음
- 회귀식 : y = 0.1210CGPA + 0.0018GRE + 0.0228LOR + 0.0246Research + 0.0030TOEFL - 1.2985

 

 

3. 단계선택법을 사용해 변수를 선택한 후 새롭게 생성한 회귀모형에 대한 잔차분석을 수행하고 그래프를 활용하여 결과를 해석하시오.

1. 모형의 선형성
- 예측값과 잔차의 비교
- 모든 예측값에서 잔차가 비슷하게 있어야함(가운데 점선)
- 빨간 실선은 잔차의 추세를 나타냄
- 빨간 실선이 점선에서 크게 벗어난다면 예측값에 따라 잔차가 크게 달라진다는 것

pred = Stepwise_best_model.predict()
residual = df['Chance_of_Admit'] - pred

sns.regplot(pred, residual, lowess=True, line_kws={'color':'red'})
plt.plot([pred.min(), pred.max()], [0,0], '--', color='grey')

 

 

2. 잔차의 정규성
- 잔차가 정규분포를 따른다는 가정
- Q-Q플롯으로 확인 가능
- 잔차가 정규분포를 띄면 Q-Q플롯에서 점선을 따라 배치되어 있어야함

import scipy.stats

sr = scipy.stats.zscore(residual)
(x,y), _ = scipy.stats.probplot(sr)
sns.scatterplot(x,y)
plt.plot([-3, 3], [-3, 3], '--', color='grey')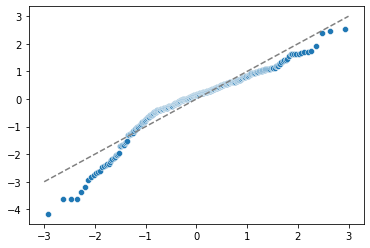

 

 

scipy.stats.shapiro(residual)
# ShapiroResult(statistic=0.9219253063201904, pvalue=1.4430034315886242e-13)

p-value값이 0.05보다 작기 때문에 유의수준 5%에서 잔차의 정규성이 위반되었다고 판단한다.

 

 

3. 잔차의 등분산성
- 회귀모형을 통해 예측된 값이 크던 작던, 모든 값들에 대해 잔차의 분산이 동일하다는 가정
- 아래 그래프는 예측값(가로축)에 따라 잔차가 어떻게 달라지는 지 보여줌
- 빨간색 실선이 수평선을 그리는 것이 이상적

sns.regplot(pred, np.sqrt(np.abs(sr)), lowess=True, line_kws={'color':'red'})

 

빨간색 실선이 수평선을 그리지 않음