adp 실기
[Python] Adp 실기 모의고사 1회 2번 파이썬 풀이(데이터에듀 교재)
ㅅ ㅜ ㅔ ㅇ
2022. 3. 19. 20:19
728x90
2. 통계분석(사용데이터: FIFA)
FIFA 데이터는 가상의 온라인 축구게임에 등장하는 축구 선수의 주요 특징과 신체 정보에 대한 데이터이며, 변수 설명은 아래와 같다.
| 변수 | 데이터형태 |
| ID | 수치형 |
| Age | 수치형 |
| Nationality | 범주형 |
| Overall | 수치형 |
| Club | 범주형 |
| Preferred Foot | 범주형 |
| Work Rate | 범주형 |
| Position | 범주형 |
| Jersey Number | 수치형 |
| Contract Valid Until | 수치형 |
| Height | 문자형 |
| Weight_lb | 수치형 |
| Release_Clause | 수치형 |
| Value | 수치형 |
| Wage | 수치형 |
1. FIFA 데이터에서 각 선수의 키는 Height변수에 피트와 인치로 입력되어 있습니다. 이를 cm로 변환하여 새로운 변수 Height_cm을 생성하시오.(" ' " 앞의 숫자는 피트이며, 뒤의 숫자는 인치, 1피트 = 30cm, 1인치 = 2.5cm)
- 데이터 불러오기
import pandas as pd
import numpy as np
data = pd.read_csv("FIFA.csv")
data.head()
- 새로운 변수 'Height_cm' 생성
data['Height_cm'] = pd.to_numeric(data['Height'].str[:1])*30 + pd.to_numeric(data['Height'].str[2:])*2.5
data.head()
2. 포지션을 의미하는 Position변수를 아래 표를 참고하여 "Forward", "Midfielder", "Defender", "GoalKeeper" 로 재범주화하고, factor형으로 변환하여 Position_Class라는 변수를 생성하고 저장하시오.
| Forward | LS, ST, RS, LW, LF, CF, RF, RW |
| Midfielder | LAM, CAM, RAM, LM, LCM, CM, RCM, RM |
| Defender | LWB, LDM, CDM, RDM, RWB, LB, LCB, CB, RCB, RB |
| GoalKeeper | GK |
- 변수 생성
data["Position_Class"] = ""
Forward = ['LS','ST','RS','LW','LF','CF','RF','RW']
MidFielder = ['LAM','CAM','RAM','LM','LCM','CM','RCM','RM']
Defender = ['LWB','LDM','CDM','RDM','RWB','LB','LCB','CB','RCB','RB']
GoalKeeper = ['GK']
for i in range(len(data)):
if data['Position'][i] in Forward:
data["Position_Class"][i] = 'Forward'
elif data['Position'][i] in MidFielder:
data["Position_Class"][i] = 'MidFielder'
elif data['Position'][i] in Defender:
data["Position_Class"][i] = 'Defender'
elif data['Position'][i] in GoalKeeper:
data["Position_Class"][i] = 'GoalKeeper'
data.head()
data['Position_Class'].value_counts()
3. 새로 생성한 Position_Class 변수의 각 범주에 따른 Value 변수 평균값의 차이를 비교하는 일원배치 분산분석을 수행하고 결과를 해석하시오. (데이터는 등분산성을 만족한다고 가정) 그리고 평균값의 차이가 통계적으로 유의하다면 사후검정을 수행하고 설명하시오.
- 귀무가설 : k개의 집단 간 모평균에는 차이가 없다.
- 대립가설 : K개의 집단 간 모평균이 모두 같다고는 할 수 없다.
- 일원배치 분산분석
import statsmodels.formula.api as smf
import statsmodels.api as sm
from statsmodels.stats.anova import AnovaRM
from scipy import stats
anova = smf.ols(formula = 'Value~Position_Class',data = data)
anova_fit = anova.fit()
anova_table = sm.stats.anova_lm(anova_fit,typ=2)
print(anova_table)
p-value값이 0.05보다 작아 귀무가설 기각 -> 사후검정 필요
- 사후검정(투키의 HSD)
from statsmodels.sandbox.stats.multicomp import MultiComparison
import scipy.stats
#투키의 HSD (유의미한 차이 분석)
from statsmodels.stats.multicomp import pairwise_tukeyhsd
hsd = pairwise_tukeyhsd(data['Value'],data['Position_Class'],alpha=0.05)
print(hsd.summary())
Forward-MidFielder의 P-value값만이 0.5609로 크게 나옴 -> 유의미한 차이x
Forward-MidFielder를 제외한 모든 변수들에 유의미한 차이가 존재한다고 판단
- 사후검정(봉페로니 교정)
#봉페로니 교정
comp = MultiComparison(data.Value,data.Position_Class)
result = comp.allpairtest(scipy.stats.ttest_ind, method = 'bonf')
print(result[0])

본페로니 방법: 유의수준 0.05를 비교하는 개수로 나누어 줍니다.
가령 3개의 그룹을 비교한다면 3개의 짝이 만들어지게 됩니다.
0.05/3=약 0.017
따라서 검정을 할 때 각 군에 대해서 유의수준 0.017을 기준으로 하게 됩니다.
Forward-MidFielder의 P-value값만이 0.2784로 크게 나옴 -> 유의미한 차이x
4. Preferred Foot과 Position_Class 변수에 따라 Value의 차이가 있는지를 알아보기 위해 이원 배치 분산 분석을 수행하고, 결과를 해석하시오.
귀무가설
- Preferred Foot 변수에 따른 Value 값 에는 차이가 없다.
- Position_Class 변수에 따른 Value 값에는 차이가 없다.
- Preferred Foot과 Position_Class변수의 상호작용 효과가 없다.
대립가설
- Preferred Foot 변수에 따른 Value 값에는 차이가 있다.
- Position_Class 변수에 따른 Value 값에는 차이가 있다.
- Preferred Foot과 Position_Class변수의 상호작용 효과가 있다.
anova2 = smf.ols(formula='Value~Preferred_Foot*Position_Class',data = data).fit()
sm.stats.anova_lm(anova2)- Preferred_Foot의 p-value값은 매우 작게 나와 귀무가설 기각 -> Value값에 영향을 미친다고 판단
- Position_Value의 p-value값은 매우 작게 나와 귀무가설 기각 -> Value값에 영향을 미친다고 판단
- Preferred_Foot:Position_Class의 p-value값 또한 매우 작게 나와 귀무가설 기각 -> 두 변수는 각 변수가 Value에 끼치는 영향도의 크기에 상호 영향을 미친다고 판단
5. Age, Overall, Wage, Height_cm, Weight_lb가 Value에 영향을 미치는지 알아보는 회귀분석을 단계적 선택법을 사용하여 수행하고 결과를 해석하시오.
variables = data[['Age','Overall','Wage','Height_cm','Weight_lb']].columns.tolist()
y = data['Value']
#선택된 변수들
selected_variables = []
sl_enter = 0.05
sl_remove = 0.05
#각 스텝별 선택 변수
sv_per_step = []
#수정된 결정계수
adjusted_r_squared = []
#스텝
steps = []
step = 0
while len(variables)>0:
remainder = list(set(variables) - set(selected_variables))
pval = pd.Series(index=remainder) ## 변수의 p-value
## 기존에 포함된 변수와 새로운 변수 하나씩 돌아가면서
## 선형 모형을 적합한다.
for col in remainder:
X = data[selected_variables+[col]]
X = sm.add_constant(X)
model = sm.OLS(y,X).fit()
pval[col] = model.pvalues[col]
min_pval = pval.min()
if min_pval < sl_enter: ## 최소 p-value 값이 기준 값보다 작으면 포함
selected_variables.append(pval.idxmin())
## 선택된 변수들에대해서
## 어떤 변수를 제거할지 고른다.
while len(selected_variables) > 0:
selected_X = data[selected_variables]
selected_X = sm.add_constant(selected_X)
selected_pval = sm.OLS(y,selected_X).fit().pvalues[1:] ## 절편항의 p-value는 뺀다
max_pval = selected_pval.max()
if max_pval >= sl_remove: ## 최대 p-value값이 기준값보다 크거나 같으면 제외
remove_variable = selected_pval.idxmax()
selected_variables.remove(remove_variable)
else:
break
step += 1
steps.append(step)
adj_r_squared = sm.OLS(y,sm.add_constant(data[selected_variables])).fit().rsquared_adj
adjusted_r_squared.append(adj_r_squared)
sv_per_step.append(selected_variables.copy())
else:
break
selected_variables
- 선택된 변수로 회귀모델 재생성
from statsmodels.stats.anova import anova_lm
reg = smf.ols('Value~Overall+Age+Wage+Height_cm',data=data).fit()
anova_lm(reg)
reg.summary2()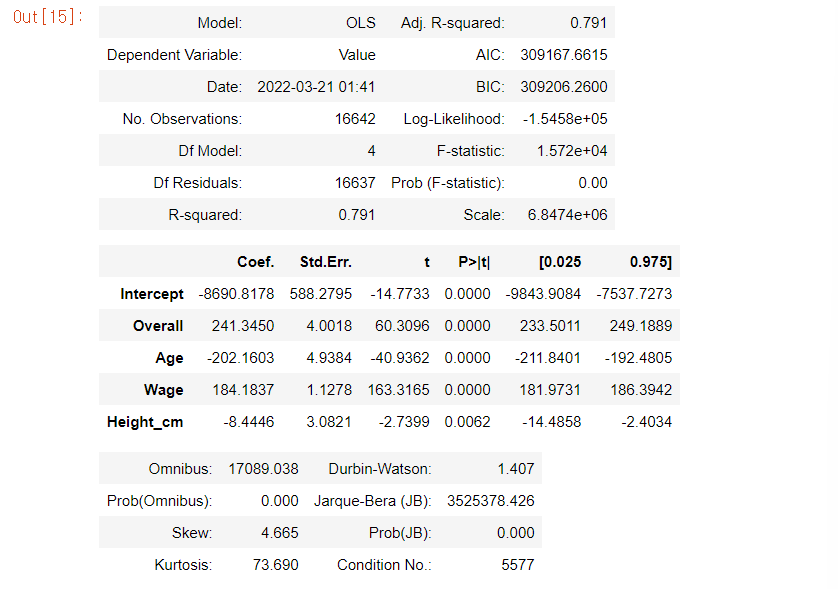
- 시각화
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,10))
fig.set_facecolor('white')
font_size = 15
plt.xticks(steps,[f'step {s}\n'+'\n'.join(sv_per_step[i]) for i,s in enumerate(steps)], fontsize=12)
plt.plot(steps,adjusted_r_squared, marker='o')
plt.ylabel('Adjusted R Squared',fontsize=font_size)
plt.grid(True)
plt.show()y = 241.345Overall - 202.1603Age + 184.184*Wage - 8.445Height_cm 이고, R-square값은 0.791이다. 즉 회귀식은 전체 데이터의 약 79.1%를 설명하고 있으며 F통계량이 0.05보다 작아 모형이 통계적으로 유의미하다고 판단할 수 있다.
회귀분석은 무조건 R로 해야겠다...ㅎㅎ

728x90